This item is taken from IGCSE Mathematics (0580) Paper 43 of May/June 2013.
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Probability
(b) Specific topic: Tree Diagrams and Dependent Events
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Probability
(b) Specific topic: Tree Diagrams and Dependent Events
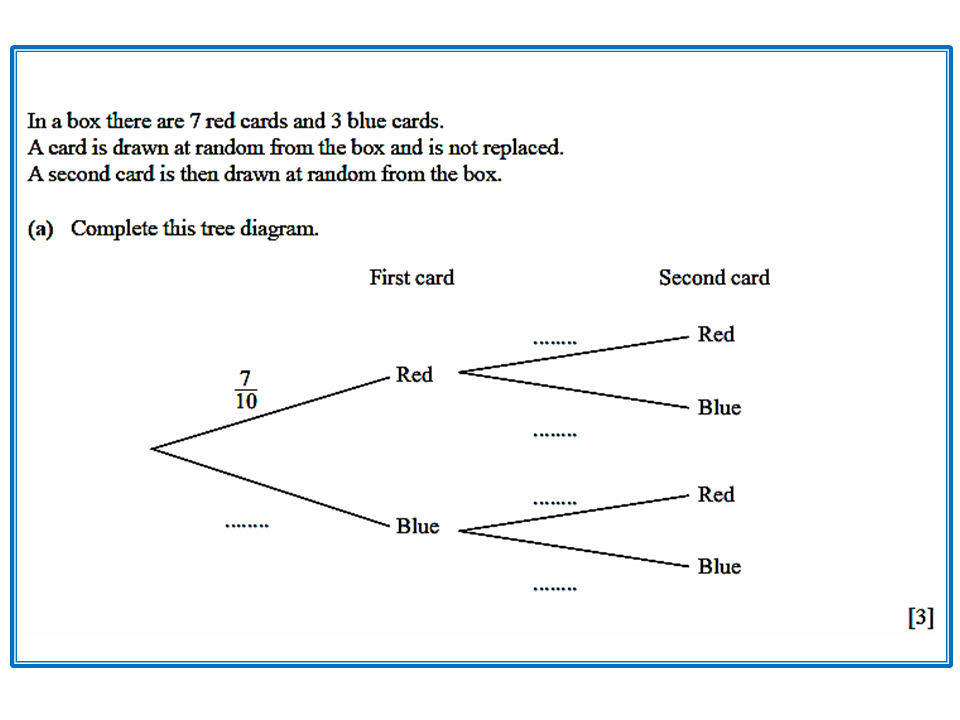
Let us take note that two cards, one at a time, are drawn at random from the box. Let us also take note that the first card chosen is not replaced in the box, which means that it is a dependent event. It means that the result on the first card chosen affects the result on the second card.
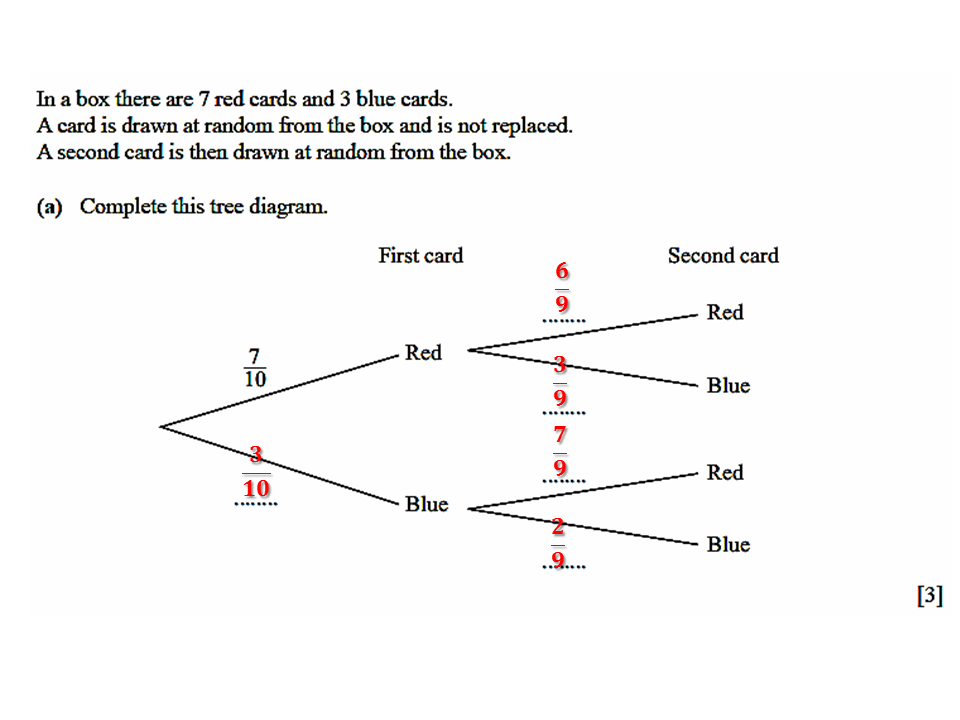
There are 3 blue cards out of 10 cards in the box so the probability that the blue card is chosen on the first pick/draw is 3/10.
Since the first card chosen is not replaced, the number of cards left in the box is decreased by one(1) for the second draw. This means that if the first card chosen is red, there will be 6 red cards and 3 blue cards left in the box. The corresponding probabilities will be
If the first card chosen is blue, there will be 7 red cards and 2 blue cards left in the box.
Therefore the complete tree diagram is
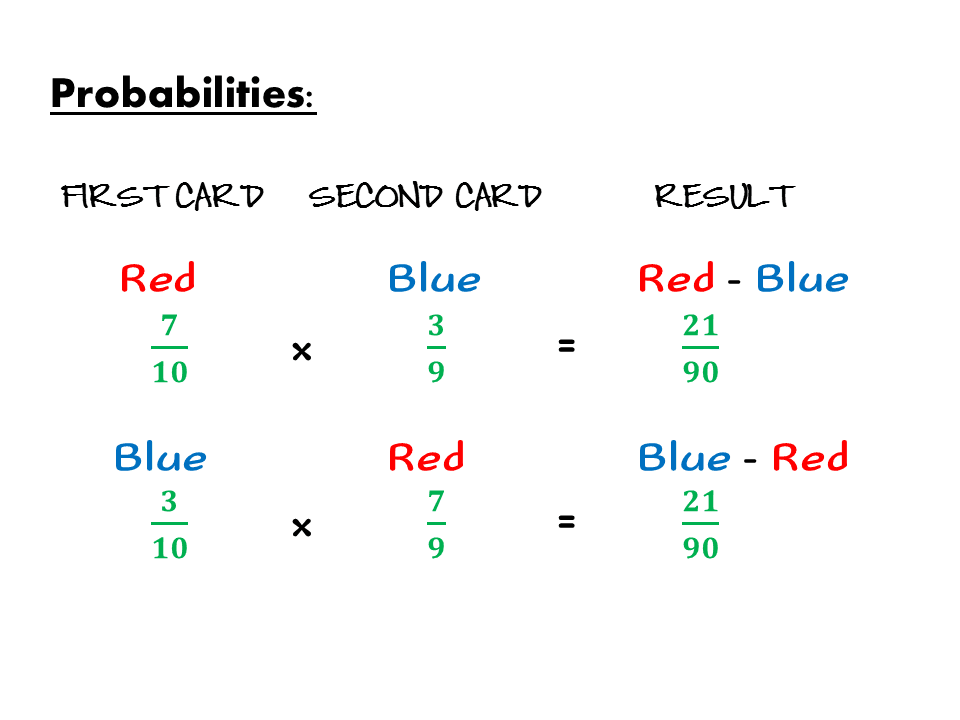
For the second question, let us take note that the two cards chosen must have different colors. The possible combinations of the cards will be
Let us look at the tree diagram for the two possible combinations of the cards.
Using the tree diagram, we can now multiply the corresponding probabilities.
Since there are two possible combinations (cases), let us add the probabilities.
Therefore, the probability that the two card have different colours is 42/90 or 7/15.
---------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. You may write them in the comment box below.
Thank you and God bless!
Thank you and God bless!















No comments:
Post a Comment