This item is taken from IGCSE Mathematics (0580) Paper 42 of May/June 2013.
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Matrices
(b) Specific topic: Operations on Matrices
The common mistake students do with this item is to get directly the square of each element of the matrix. Here is the common wrong solution and answer:
Take note that:
It means that it is the product of matrix D multiplied to itself.
Before you start multiplying, determine first the order (dimension) of each matrix and the order of the resulting matrix.
It is possible to multiply the matrices since the number of columns of the first is equal to the number of rows of the second matrix. Follow the method of multiplying matrices - multiply each row of the first to each column of the second. That is
Simplify.
Therefore,
----------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!
www.mathematicsrealm.blogspot.com
www.learnatmathematicsrealm.blogspot.com
www.igcseatmathematicsrealm.blogspot.com
www.ciemathsolutions.blogspot.com
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Matrices
(b) Specific topic: Operations on Matrices
The common mistake students do with this item is to get directly the square of each element of the matrix. Here is the common wrong solution and answer:
Take note that:
It means that it is the product of matrix D multiplied to itself.
Before you start multiplying, determine first the order (dimension) of each matrix and the order of the resulting matrix.
It is possible to multiply the matrices since the number of columns of the first is equal to the number of rows of the second matrix. Follow the method of multiplying matrices - multiply each row of the first to each column of the second. That is
Simplify.
Therefore,
----------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!
www.mathematicsrealm.blogspot.com
www.learnatmathematicsrealm.blogspot.com
www.igcseatmathematicsrealm.blogspot.com
www.ciemathsolutions.blogspot.com



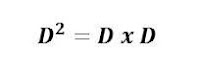
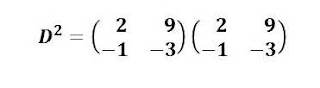



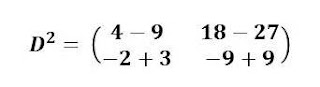








No comments:
Post a Comment