This item is taken from IGCSE Mathematics (0580) Paper 2 of October/November 2007.
To deal with this item, let us summarize the details of the problem:
(a) Syllabus area: Vectors
(b) Specific topic: Addition/Subtraction of Vectors, Position Vectors, Naming a Vector in Terms of other Two Vectors
(c) Concepts Needed: Triangle Law for Addition/Subtraction of Vectors
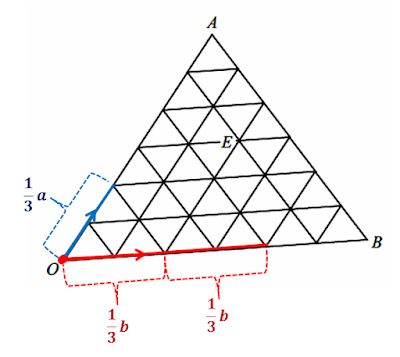
To answer (i), take note that vector OA = a and vector OB = b. Let us divide each vector into three parts as shown:
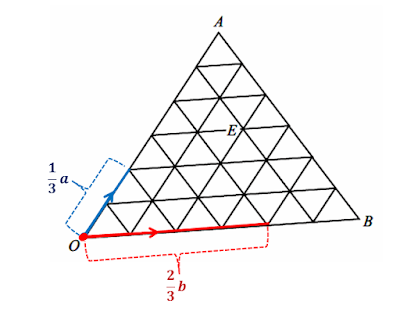
Since we need 1/3 of a, we will take 1 part of a. On the other hand, we need 2/3 of b, meaning 2 parts of b.
Here are the vectors 1/3 a and 2/3 b:
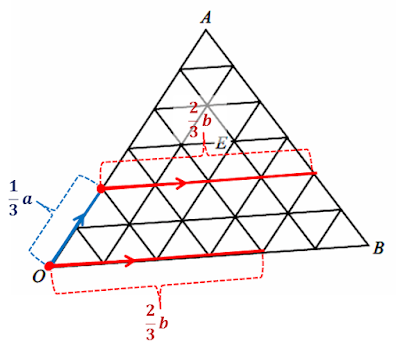
Following the triangle law of addition for vectors, the end of the first vector should be the start of the second vector. This means that the the tip of 1/3 a should be the start of 2/3 b.
From this, we can now draw the resulting vector 1/3 a + 2/3 b.
However, we are finding point C, which is the tip/end of this resulting vector.
Therefore, point C is located at
-------------------------------------------------------------------------------------------------------------------------------
Your comments and suggestions are welcome here. Write them in the comment box below.
Thank you and God bless!
3 comments:
Here's a superb personalized online math practice platform @ http://www.begalileo.com
Thank you, that was just an awesome post!!!
Thank you indeed
Post a Comment